Compute Curvature Flow#
Synopsis#
Denoise an image using curvature driven flow.
Results#
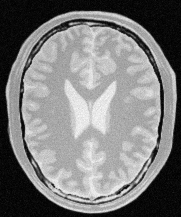
Input image#
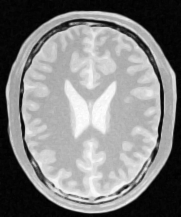
Output image#
Code#
Python#
#!/usr/bin/env python
import itk
import argparse
parser = argparse.ArgumentParser(description="Compute Curvature Flow.")
parser.add_argument("input_image")
parser.add_argument("output_image")
parser.add_argument("number_of_iterations", type=int)
parser.add_argument("time_step", type=float)
args = parser.parse_args()
InputPixelType = itk.F
OutputPixelType = itk.UC
Dimension = 2
InputImageType = itk.Image[InputPixelType, Dimension]
OutputImageType = itk.Image[OutputPixelType, Dimension]
ReaderType = itk.ImageFileReader[InputImageType]
reader = ReaderType.New()
reader.SetFileName(args.input_image)
FilterType = itk.CurvatureFlowImageFilter[InputImageType, InputImageType]
curvatureFlowFilter = FilterType.New()
curvatureFlowFilter.SetInput(reader.GetOutput())
curvatureFlowFilter.SetNumberOfIterations(args.number_of_iterations)
curvatureFlowFilter.SetTimeStep(args.time_step)
RescaleFilterType = itk.RescaleIntensityImageFilter[InputImageType, OutputImageType]
rescaler = RescaleFilterType.New()
rescaler.SetInput(curvatureFlowFilter.GetOutput())
outputPixelTypeMinimum = itk.NumericTraits[OutputPixelType].min()
outputPixelTypeMaximum = itk.NumericTraits[OutputPixelType].max()
rescaler.SetOutputMinimum(outputPixelTypeMinimum)
rescaler.SetOutputMaximum(outputPixelTypeMaximum)
WriterType = itk.ImageFileWriter[OutputImageType]
writer = WriterType.New()
writer.SetFileName(args.output_image)
writer.SetInput(rescaler.GetOutput())
writer.Update()
C++#
#include "itkImageFileReader.h"
#include "itkImageFileWriter.h"
#include "itkCurvatureFlowImageFilter.h"
#include "itkRescaleIntensityImageFilter.h"
int
main(int argc, char * argv[])
{
if (argc != 5)
{
std::cerr << "Usage: " << std::endl;
std::cerr << argv[0];
std::cerr << " <InputFileName> <OutputFileName>";
std::cerr << " <numberOfIterations> <timeStep>";
std::cerr << std::endl;
return EXIT_FAILURE;
}
const char * inputFileName = argv[1];
const char * outputFileName = argv[2];
constexpr unsigned int Dimension = 2;
using InputPixelType = float;
using InputImageType = itk::Image<InputPixelType, Dimension>;
using OutputPixelType = unsigned char;
using OutputImageType = itk::Image<OutputPixelType, Dimension>;
const int numberOfIterations = std::stoi(argv[3]);
const InputPixelType timeStep = std::stod(argv[4]);
const auto input = itk::ReadImage<InputImageType>(inputFileName);
using FilterType = itk::CurvatureFlowImageFilter<InputImageType, InputImageType>;
auto filter = FilterType::New();
filter->SetInput(input);
filter->SetNumberOfIterations(numberOfIterations);
filter->SetTimeStep(timeStep);
using RescaleType = itk::RescaleIntensityImageFilter<InputImageType, OutputImageType>;
auto rescaler = RescaleType::New();
rescaler->SetInput(filter->GetOutput());
rescaler->SetOutputMinimum(itk::NumericTraits<OutputPixelType>::min());
rescaler->SetOutputMaximum(itk::NumericTraits<OutputPixelType>::max());
try
{
itk::WriteImage(rescaler->GetOutput(), outputFileName);
}
catch (const itk::ExceptionObject & error)
{
std::cerr << "Error: " << error << std::endl;
return EXIT_FAILURE;
}
return EXIT_SUCCESS;
}
Classes demonstrated#
-
template<typename TInputImage, typename TOutputImage>
class CurvatureFlowImageFilter : public itk::DenseFiniteDifferenceImageFilter<TInputImage, TOutputImage> Denoise an image using curvature driven flow.
CurvatureFlowImageFilter implements a curvature driven image denoising algorithm. Iso-brightness contours in the grayscale input image are viewed as a level set. The level set is then evolved using a curvature-based speed function:
where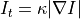
 is the curvature.
is the curvature.
The advantage of this approach is that sharp boundaries are preserved with smoothing occurring only within a region. However, it should be noted that continuous application of this scheme will result in the eventual removal of all information as each contour shrinks to zero and disappear.
Note that unlike level set segmentation algorithms, the image to be denoised is already the level set and can be set directly as the input using the SetInput() method.
This filter has two parameters: the number of update iterations to be performed and the timestep between each update.
The timestep should be “small enough” to ensure numerical stability. Stability is guarantee when the timestep meets the CFL (Courant-Friedrichs-Levy) condition. Broadly speaking, this condition ensures that each contour does not move more than one grid position at each timestep. In the literature, the timestep is typically user specified and have to manually tuned to the application.
This filter make use of the multi-threaded finite difference solver hierarchy. Updates are computed using a CurvatureFlowFunction object. A zero flux Neumann boundary condition when computing derivatives near the data boundary.
This filter may be streamed. To support streaming this filter produces a padded output which takes into account edge effects. The size of the padding is m_NumberOfIterations on each edge. Users of this filter should only make use of the center valid central region.
Reference: “Level Set Methods and Fast Marching Methods”, J.A. Sethian, Cambridge Press, Chapter 16, Second edition, 1999.
- Warning
This filter assumes that the input and output types have the same dimensions. This filter also requires that the output image pixels are of a floating point type. This filter works for any dimensional images.
Input/Output Restrictions: TInputImage and TOutputImage must have the same dimension. TOutputImage’s pixel type must be a real number type.
- See
DenseFiniteDifferenceImageFilter
- See
CurvatureFlowFunction
- See
MinMaxCurvatureFlowImageFilter
- See
BinaryMinMaxCurvatureFlowImageFilter
- ITK Sphinx Examples:
Subclassed by itk::MinMaxCurvatureFlowImageFilter< TInputImage, TOutputImage >
